Publications
While working as a physicist I am interested in astrophysics and cosmology. My research interests include theoretical cosmology, dark energy, modified gravity, non-linear perturbation theory, software development for analysing datasets, statistical methods in cosmology, the Hubble constant, neutrino mass, large scale structure, gravitational waves, N-body simulations, and machine learning techniques applied to cosmology. Actually I would like to test every interesting cosmological model against current and future probes.
A few of my publications can be found below. For a full list please visit iNSPIRE, arXiv, ads
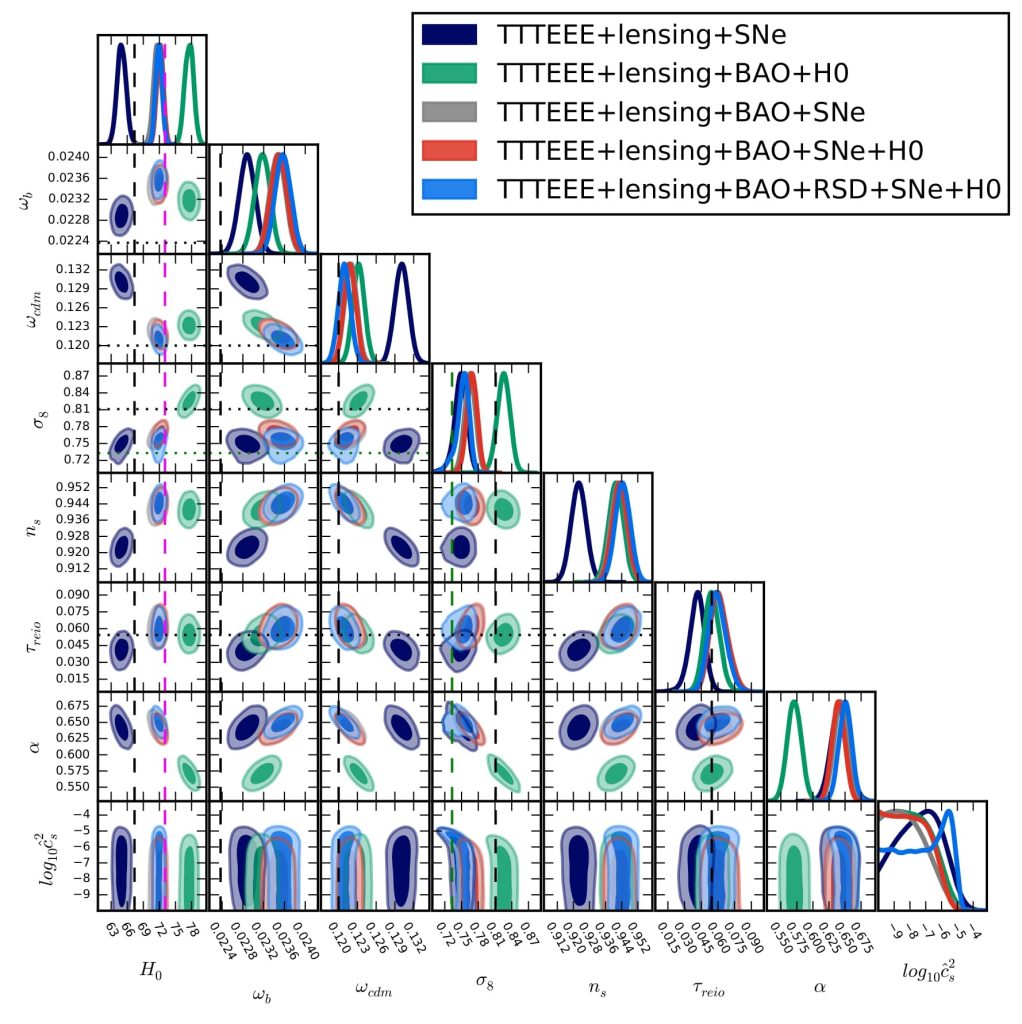
Varying Dark Energy equation of state, Dark Energy sound speed, and Tensions in cosmological parameters: H0 and S8
In this paper we showed that a varying dark energy equation of state along with a non trivial dark energy sound speed can alleviate current tensions in cosmological parameters such as the Hubble constant H0 and the strength of matter clustering S8. The figure shows 1D marginalised posteriors as well as confidence contours for a holographic dark energy model
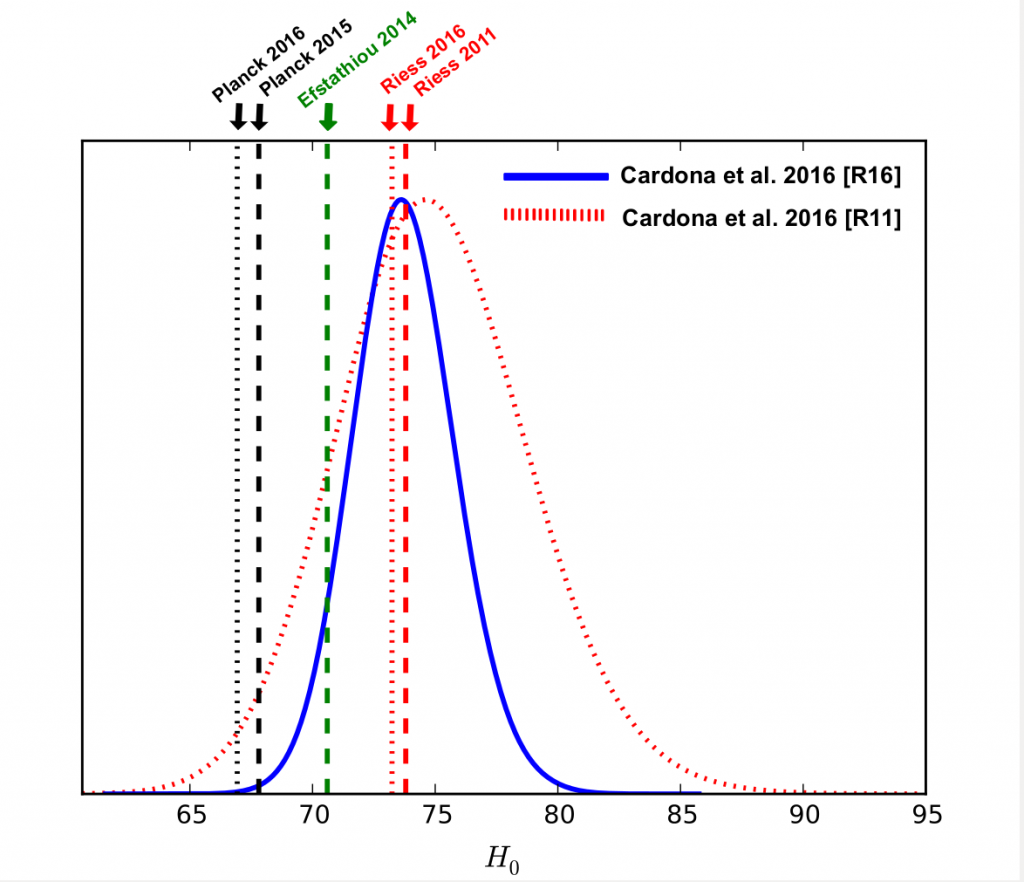
Pinning down the Hubble constant
In this project we developed a new statistical method to measure the Hubble constant. Our approach avoids the use of outlier rejection algorithms and allows to assess consistency of datasets. The figure shows our posterior probability density of the Hubble constant compared to other determinations of Ho. Below a pretty interesting talk by Nobel Laureate Adam Riess where a comparison with our work is discussed.
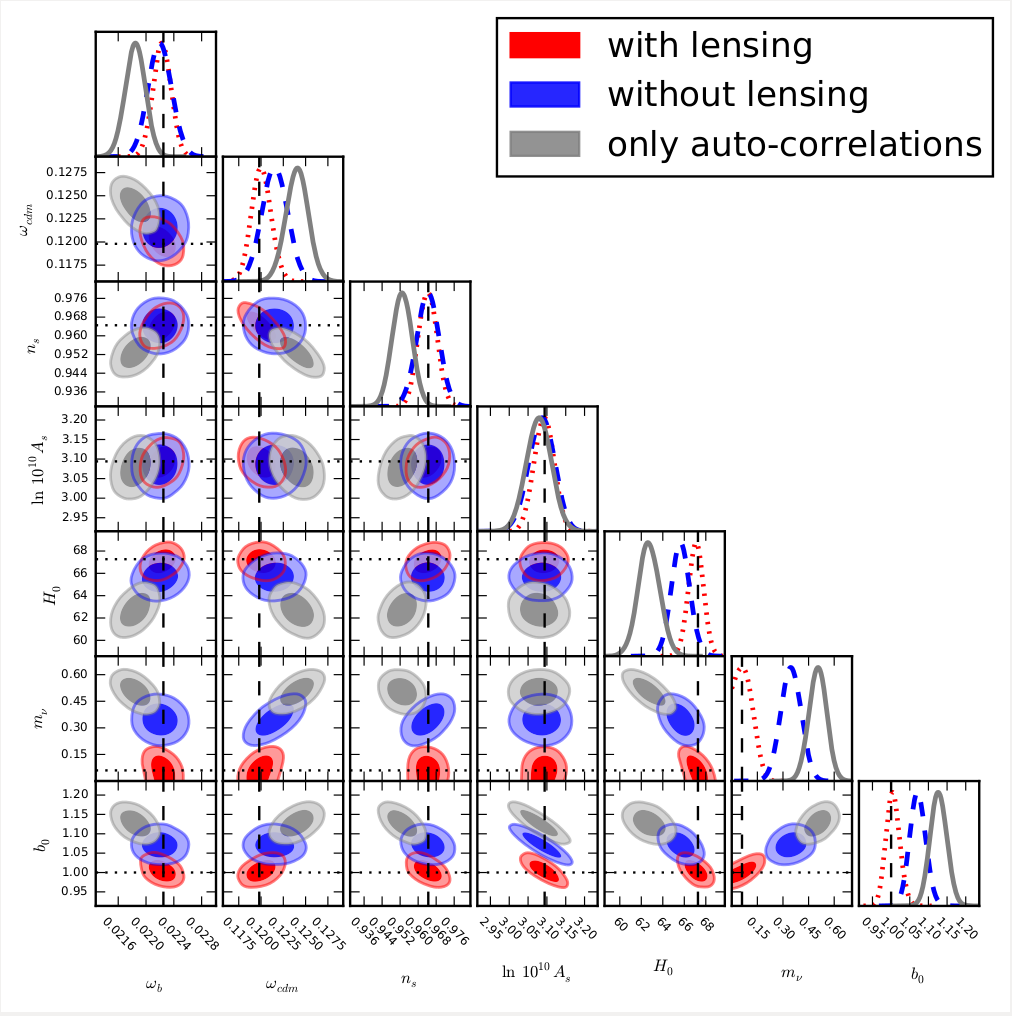
The relevance of lensing convergence when constraining neutrino masses
In this project we showed the importance of including the lensing contribution in galaxy clustering analyses with large galaxy redshift surveys. We considered an Euclid-like galaxy survey and demonstrated that neglecting lensing convergence severely biases cosmological parameter estimation with redshift surveys. It leads to significant shifts for several cosmological parameters, most notably the scalar spectral index and the neutrino mass scale. Especially the latter parameter is one of the main targets of future galaxy surveys. The figure shows 1D and 2D posterior probabilities for a proper analysis including lensing convergence (red) along with an incorrect analysis neglecting lensing convergence (blue)
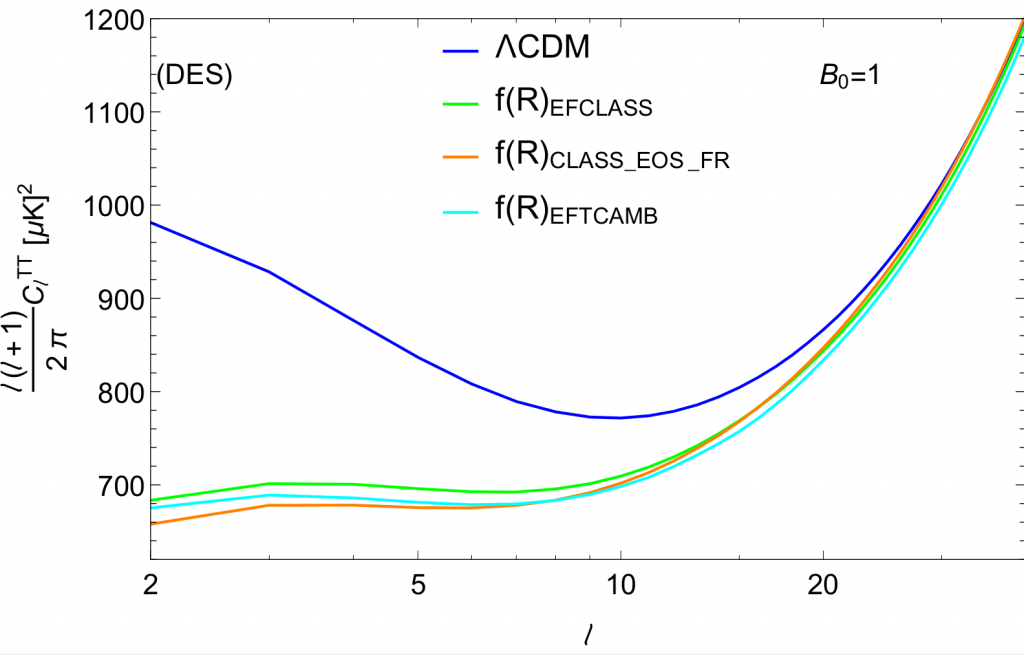
Unraveling the effective fluid approach for f(R) models
In this project we provided explicit formulae for the effective fluid description of f(R) models. We also carried out the implementation in the popular Boltzmann solver CLASS and make it publicly available. Our approach is less error-prone than other implementations and properly takes into account the variation of the background evolution in general f(R) models. The figure shows the CMB angular power spectrum for a designer w=-1 f(R) model. We compare the outputs from different Boltzmann solvers.
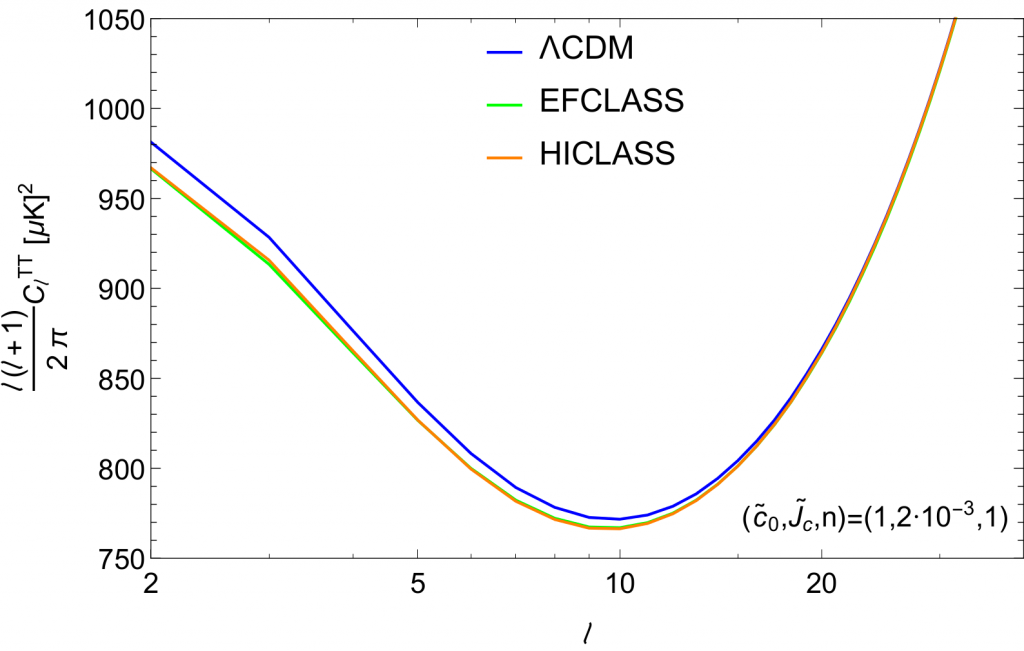
Designing Horndeski
We managed to generalise our effective fluid approach to Horndeski theories. As a result we found formulae for the effective fluid description of these kinds of models which allow a less error-prone implementation in Boltzmann solvers. By using our approach we found a family of viable models which match the background evolution of the standard cosmological model while having different evolution of the perturbations. The figure shows the CMB angular power spectrum for a designer w=-1 Horndeski model. We compare outputs from EFCLASS (our effective fluid approach) and Hi-CLASS. The latter does not use any approximations, whereas EFCLASS uses sub-horizon and quasi-static approximations. The agreement of the two implementations is remarkable.
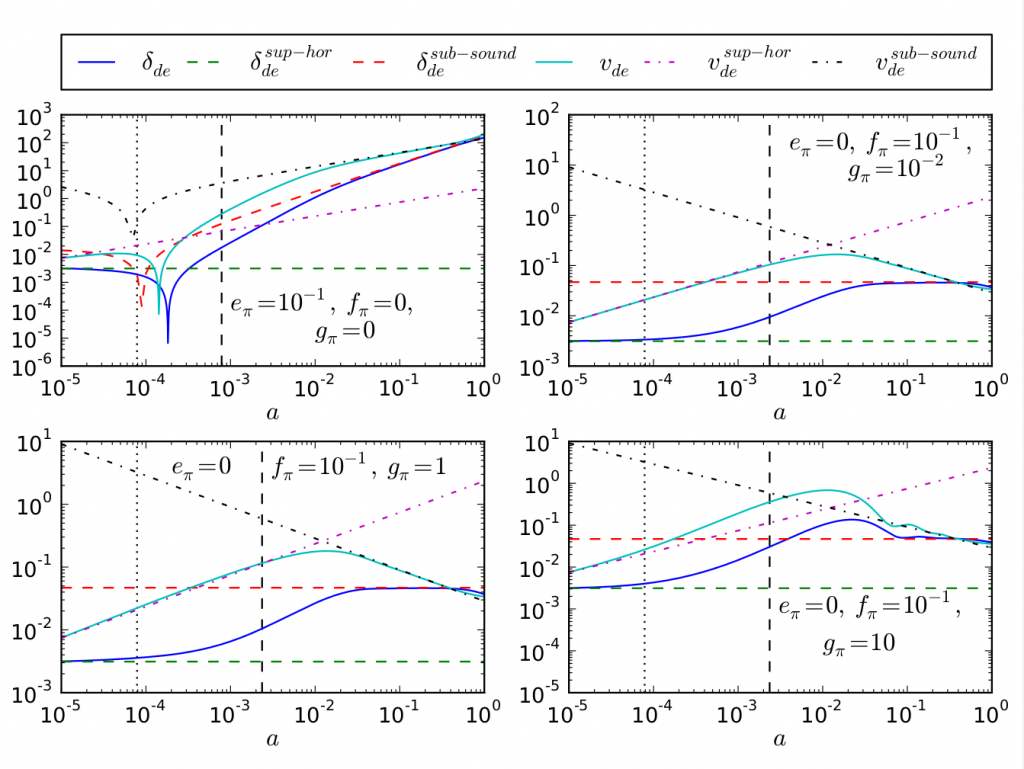
The traces of anisotropic dark energy
In this project we investigated a cosmological model including a non-vanishing dark energy anisotropic stress. We found approximated, analytical solutions for the evolution of dark energy perturbations in different regimes (e.g., dark matter and dark energy dominance). By using data from the Planck Collaboration as well as other available data sets we found tight constraints for models where dark matter perturbations act as a source of dark energy anisotropic stress. The figure shows the evolution of Dark Energy perturbations in a cosmological model including a non-vanishing dark energy anisotropic stress.